Ms. Price
|
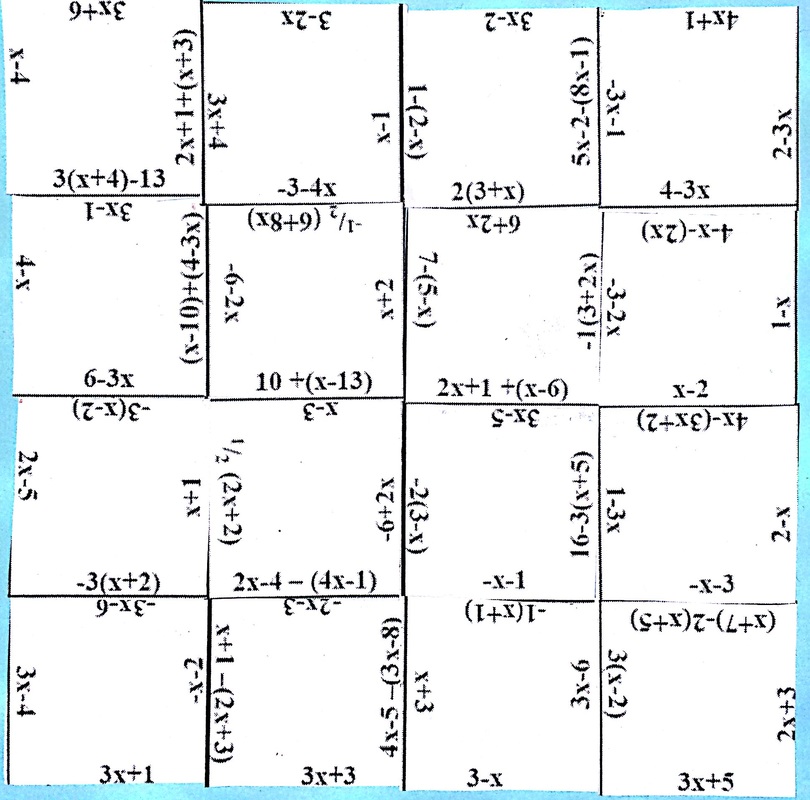
The Algebraic Puzzle was given as an assignment for students to demonstrate their understanding of the distributive property, combining like terms, and integer operations to simplify expressions. This assignment was the only item other than "I Already Know" for this journal entry. The work for the assignment should be either on the journal entry page itself or on the puzzle pieces.
0 Comments
We completed 10 problems and reviewed the answers by having the most common answer as each team's final answer to see which team would get the most correct. In class, we reviewed #1 incorrectly and the correct answer is updated here. *1) 3 – 3(x -2) 3-3x + 6 --->>> -3x + 9 2) –(1 – 5n) – 7n -1 + 5n - 7n --->>> -1 - 2n 3) 8 + 7(7n – 4) 8 + 49n - 28 --->>> 49n - 20 4) 4x + 5(3x -3) 4x + 15x - 15 --->>> 19x - 15 5) 1 – 8x – 5x 1 + -8x + -5x --->>> 1 - 13x 6) 5 – 2(8x + 4) 5 + -2(8x+4) ---> 5 + - 16x + - 8 --->>> -3 - 16x 7) 7 + 6x + 9(x + 1) 7 + 6x + 9x + 9 --->>> 15x + 16 8) -3 + 8x + 2 8x - 1 9) 5 – 8n – 4n -12n + 5 10) 9 + 3x + 1 – 2x x + 10 The homework below also uses this skill and most students completed the homework in class during the stations activity. The stations activity dealt with evaluating expressions (substitution).
A few warm-ups have been used to prep for this skill, and it is simple plug-in and use the order of operations. Below is an example to illustrate how to use substitution.
Ex. -3x^2 +4 if x = -2 1) Plug in -2 everywhere that x exists. The -2 is traded in for the x and x is no longer in the expression. -3(-2)^2 + 4 2) Understand what substituting the value for the variable means: The coefficient for x means to multiply the variable (-2) by -3 since there are 3 groups of x. The exponent was directly beside the variable so the base for the exponent can only be -2. We have discussed the difference between (-3x)^2 and -3x^2 where the first example means to square everything within the parentheses to get 9x^2 and the second example only squares the variable and not the coefficient. 3) Use the order of operations to solve. P - Nothing to do within the parentheses here. Also note the parentheses are optional and were added to show the number inside was negative to separate it from the rest of the problem. E - The exponent can be worked since we have a value for x now so (-2)^2 is 4. MD - From left to right, we have multiplication of -3*4 = -12. AS - From left to right, we have addition of -12 + 4 = -8. We used a silent stations activity to practice this skill. Students completed a half sheet of paper (8 questions with 1 question already worked as an example) on evaluating expressions that should be stapled into this journal entry.
Much of this topic, we already know so the I Already Know section functions as notes here.
We will be using what we know about how the distributive property works as well as how to multiply positive and negative numbers. We learned how to write a verbal expression of each algebraic expression: -2(x + 4) the opposite of two groups of x plus four Answer: -2x - 4 -3(x – 6) the opposite of three groups of x minus six Answer: -3x + 18 The video provided us with examples in the first 6 minutes directly related to this topic. We worked select problems from this worksheet, #2, 6, 7, 10, 13, 15 Then we practiced expanding and then simplifying these problems: 1) 2(x – 8) 2) -5(x + 9) 3) -3(x – (-3)) 4) -6(-2x + 5) 5) -3(-2x – 4)
With this journal entry, you found the notes on your own by completing your homework given on 9/4. This journal entry is a compilation of the resources we used to add to our notes. There were no essential questions for this journal entry.
NOTES; There are rules to multiplying integers. The same rules of multiplication apply to division. The first site that should be visited to be acquainted with these rules is HERE. The explanations are clear, and the visuals are good to help you understand. The video below shows a "shortcut" for remembering the rule to multiplying and dividing integers.
The PBS Math Club video explains the interaction and the product result of multiplying integers. It is also good to use for understanding word problems.
The link to Braining Camp shows an interactive way through counters and number lines that tries to explain what is happening during a multiplication of integers problem.
PRACTICE; KhanAcademy had great practice problems that we solved in pairs. We also worked on IXL's fill-in-the-blank problems, although you need an account after a certain number of problems. We also discussed how to solve problems with more than 2 factors, and we worked through word problems as shown in the PowerPoint slides. We then used Kahoot! to check our understanding one more time in class.
Essential Question:
How is subtraction of integers similar or different from addition of integers? Notes: On Review WS. Subtracting a positive number = adding a negative number by using the additive inverse. The additive inverse just says to change subtraction to addition, and flip the sign of the next number to its opposite. Subtraction problems are the ONLY problems that you perform the additive inverse with. Practice: #2, 3, 7, 8 on Review Integers WS and problems from PowerPoint listed as Other Practice Problems **Completed Exit Ticket**
Essential Questions:
What kind of numbers are rational numbers? Are all integers called rational numbers also? Notes: Rational numbers are basically any number, positive or negative, that can be written as a fraction. Repeating decimals are rational numbers. Practice: Which of these are rational numbers? 3 -1.7777 ∞ 2/3 2.8 pi 1.567 repeating Why? Answer: All are rational numbers except infinite and pi. Order these rational numbers from least to greatest: -1.2 -0.1 -3/8 -1.01 -2/11 -1/6 How did you find out the correct order? There are 2 strategies that mathematically prove the order of these numbers. 1) Change the numbers so that you can compare them using common denominators. 2) Change the numbers into decimals by dividing the fractions (top goes in the house). Answer: -1.2 -1.01 -3/8 -2/11 -1/6 -0.1 Essential Questions:
What are the steps of the order of operations? Why do we have an order of operations in math? Notes: PEMDAS. Multiply AND divide go together, whichever comes first in the problem from left to right. Add AND subtract go together, whichever comes first in the problem from left to right. Practice: https://drive.google.com/a/wcpss.net/file/d/0B7QFTBrrB9NOMGI3S1dNbGhibms/view?usp=sharing |
ArchivesCategories |
||||||||||||||||||||||||||||||||||||||||||||||||
 RSS Feed
RSS Feed
